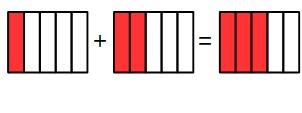
When fractions have the same denominator we can add them together (or subtract one from the other).
If we add one fifth and add two fifths we will have three fifths
If we have 3 quarters and we take away 2 quarters we have 1 quarter left
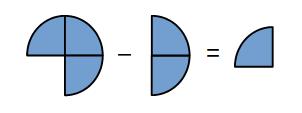
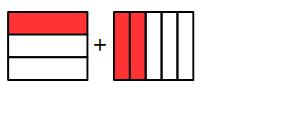
Try these:
When we do not have fractions with the same denominator we need to make the denominators the same before we can add them (or take them away).
We can make denominators the same using equivalent fractions.
Example:
To add these fractions we need to make the denominators the same.
To make the denominators the same we need to find a number that is in both the 3 and the 5 times tables. 15 is the lowest number in both the 3 and 5 times tables.
We need to multiply the denominator of
We multiply the numerator and denominator of
Now both fractions have the same denominators we can add them:
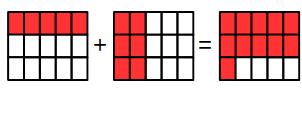
Example:
To subtract these fractions we need to make the denominators the same.
To make the denominators the same we need a number that is in the 4 and 6 times tables. The smallest number in the 4 and 6 times tables is 12 (If we used another number in both times tables the answer would still be correct, the working out would just be more difficult).
We need to multiply the numerator and denominator of
We need to multiply the numerator and denominator of
Now both fractions have the same denominators we can subtract them:
Try these:
All answers are given in their simplest form
When we have mixed numbers we can change the mixed numbers to improper (top heavy) fractions before adding (or subtracting) the fractions.
Example: 1
The mixed number we have here is 1
One whole is the same as 4 quarters.
Therefore we have:
We can change the question to:
To make the denominators the same we multiply the top and bottom of
We could leave our answer as an improper fraction or convert it back to a mixed number.
To convert
12 goes into 29 2 times (with 5 left over)
Try these:
All answers are given in their simplest form
To multiply fractions we multiply the numerators and multiply the denominators.
Example:
We multiply the numerators and multiply the denominators
We can simplify our answer by dividing the numerator and the denominator by 2
When we have mixed numbers we need to convert them to top heavy fractions (improper) before we can multiply them
Example: 1
One whole is the same as three thirds.
3 thirds and 2 thirds make 5 thirds.
1
We can now multiply the numerators and multiply the denominators
Try these:
All answers are given in their simplest form
Division is the opposite operation to multiplication
Multiplying by
Multiplying by
We can divide fractions by multiplying the first fraction by the second fraction flipped over (the reciprocal of the second fraction).
Example:
We can simplify the answer by dividing the top and bottom by 2
When we have mixed numbers we need to convert them to improper fractions before dividing the fractions
Example:
We need to convert 2
2 is the same as
We now have:
Dividing by
Try these:
All answers are given in their simplest form
GCSE
Learn GCSE MathsA Level
Learn A Level MathsCopyright © Maths Genie. Maths Genie Limited is a company registered in England and Wales with company number 14341280. Registered Office: 86-90 Paul Street, London, England, EC2A 4NE.