When we use error intervals we are looking at a number that has been rounded. An error interval tells us the range of numbers that we could have had before the number was rounded.
Example 1: A number x has been rounded to one decimal place
The result is 4.8
Write down the error interval for x
The number has been rounded to 4.8 to one decimal place.
The number below is 4.7 and the number above is 4.9 (to one decimal place)
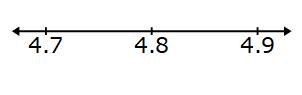
We need to look half way between 4.7 and 4.8 for the lower bound and half way between 4.8 and 4.9 for the upper bound.

The number must have been between 4.75 and 4.85 to round to 4.8 to one decimal place.
This can be written as an inequality.
4.75 would round to 4.8, so we use an or equal symbol
4.85 would not round to 4.8 we just use the less than symbol.
4.75 ≤ x < 4.85
Example 2: A number y has been rounded to one significant figure
The result is 7000
Write down the error interval for y
The number below is 6000 and the number above is 8000 (to one significant figure)
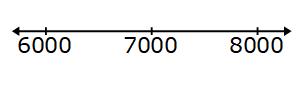
We need to look half way between 6000 and 7000 for the lower bound and half way between 7000 and 8000 for the upper bound.
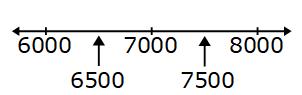
The number must have been between 6500 and 7500 to round to 7000 to one significant figure.
We write this as an inequality. The number could have been equal to 6500, but not equal to 7500.
6500 ≤ y < 7500
Try these:
When a number has been truncated it has been cut off. If we truncate a number to one decimal place we delete all digits after one decimal place. If we truncate a number to two decimal places we delete all digits after two decimal places.
Example 3: Truncate 4.5891 to one decimal place
We delete all the digits after one decimal place:
4.5891
4.5891 truncated to one decimal place is 4.5
Example 4: Truncate 19.68572 to two decimal places
We remove all the digits after two decimal places:
19.68572
19.68572 truncated to two decimal place sis 19.68
Example 5: A number x has been truncated to one decimal place
The result is 1.4
Write an error interval for x
The number must have began with 1.4 in order for it to be truncated to 1.4

All of the numbers between 1.4 and 1.5 begin with 1.4
The number could have been equal to 1.4 but not equal to 1.5 (It could have been anything up to 1.5, but not 1.5)
1.4 ≤ x < 1.5
Try these:
GCSE
Learn GCSE MathsA Level
Learn A Level MathsCopyright © Maths Genie. Maths Genie Limited is a company registered in England and Wales with company number 14341280. Registered Office: 86-90 Paul Street, London, England, EC2A 4NE.