Angles

Angles on a straight line add to 180°

Example 1: Find the size of angle a

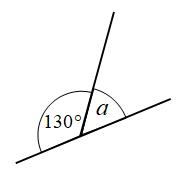
Angles on a straight line add to 180°
a + 130° = 180°
a = 50°

Example 2: Find the size of angle b

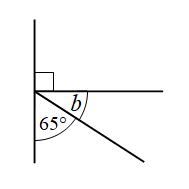
Angles on a straight line add to 180°
b + 90° + 65° = 180°
b + 155° = 180°
b = 25°

Try these:

Find the size of angle c:

Find the size of angle d:

Angles around a point add to 360°

Example 3: Find the size of angle e

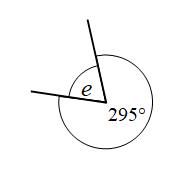
Angles around a point add to 360°
e + 295° = 360°
e = 65°

Example 4: Find the size of angle f

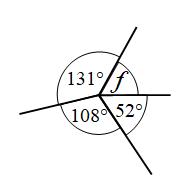
Angles around a point add to 360°
f + 131° + 108° + 52° = 360°
f + 291° = 360°
f = 69°

Try these:

Find the size of angle g:

Angles in a triangle add to 180°

Example 5: Find the size of angle j

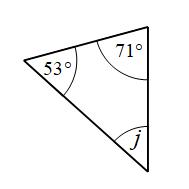
Angles in a triangle add to 180°
j + 71° + 53° = 180°
j + 124° = 180°
j = 56°

Example 6: Find the size of angle k

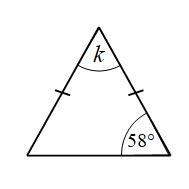
Here we have an isosceles triangle. In an isosceles triangle two angles (and two sides) are equal.
There are lines on two of the sides to show that they are equal. The other side of an isosceles triangle is called the base.
The angles at the base of an isosceles triangle are equal. This means we have two 58° angles.

k + 58° + 58° = 180°
k + 116° = 180°
k = 64°

Example 7: Find the size of angle m

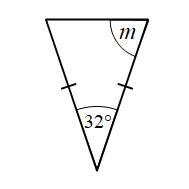
We have another isosceles triangle. This time the missing angle is at the base.

m + m + 32° = 180°
2m = 148°
m = 74°

Try these:

Find the size of angle n:

Find the size of angle p:

Find the size of angle q: